Предельное сопротивление основания соответствует полному исчерпанию грунтом несущей способности и сплошному развитию зон предельного равновесия, что достигается для оснований сооружений при окончании формирования жесткого ядра, деформирующего основание и распирающего грунт в стороны. Различают предельные сопротивления грунта основания в стабилизированном, когда осадка закончилась, и нестабилизированном состояниях.
В стабилизированном состоянии отсутствует избыточное поровое давление воды, предельное сопротивление грунта выше, чем в нестабилизированном. Предельное сопротивление грунта в нестабилизированном состоянии зависит от степени его консолидации. Чем выше степень консолидации грунта основания, тем выше его сопротивление, выпирающее из-под подошвы сооружения (по Ю.А. Соболевскому, 1986).
Предельное сопротивление основания, сложенного нескальными грунтами, в стабилизированном состоянии определяется исходя из условия, что соотношение между нормальными σ и касательными τ напряжениями по всем поверхностям скольжения, соответствующего предельному состоянию основания, подчиняется зависимости Кулона:
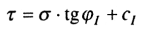
где φI — расчетное значение угла внутреннего трения (индекс I означает, что расчет производится по первой группе предельных состояний); сI— расчетное значение удельного сцепления грунта.
Для определения предельного сопротивления грунта Рu основания в настоящее время используются приближенные расчетные методы, разработанные главным образом для условий плоской или осесимметричной задач.
Впервые задача о предельном давлении на невесомый грунт в условиях плоской задачи была решена Прандтлем и Рейсснером (1920—1921) по схеме, показанной на рис. 8.6. Для грунта, обладающего трением и сцеплением, формулу Прандтля и Рейсснера Н.А. Цытович приводит в виде:
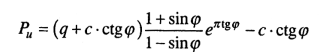 (8.31)
(8.31)
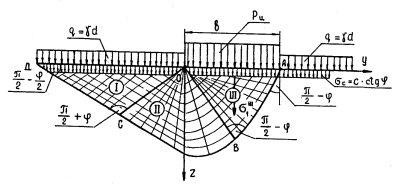
Рис. 8.6. Схема линий скольжения при предельной полосовой нагрузке
На рис. 8.6 показаны линии скольжения в невесомой среде (γ = 0) при предельной полосовой нагрузке. В этом случае, непосредственно под нагрузкой, где сг действует в вертикальном направлении, два семейства пересекающихся поверхностей скольжения образуют в зоне ОАВ вертикальные ромбы (область III). В зоне ОВС, как доказано Прандтлем и Рейсснером,спирали. Далее в зоне ОСД образуются также ромбы (область I), но горизонтальные, так как здесь наибольшее главное напряжение направлено горизонтально. Угол выхода граничной линии области предельного равновесия на поверхность основания составляет
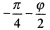
Предельное давление для идеально связных грунтов (φ = 0, с≠0) при условии:
плоской задачи (по Прандтлю)
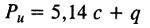 (8.32)
(8.32)
осесимметричной задачи (по А.Ю. Ишлинскому, 1947)
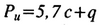 (8.33)
(8.33)
осесимметричной задачи для водонасыщенных связных грунтов (по А.С. Строганову, 1977)
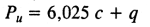 (8.34)
(8.34)
Для оснований массивных фундаментов предельную нагрузку необходимо определять с учетом уплотненного ядра грунта, формирующегося под подошвой жестких фундаментов в виде прямоугольного треугольника. Тогда очертание обертывающих поверхностей скольжения под жестким круглым фундаментом будет соответствовать схеме, изображенной на рис. 8.7. Согласно расчетной методике В.Г. Березанцева, угол наклона уплотненного ядра к подошве фундамента принимается равным 8 δ = π/4
Рис. 8.7. Схема линий скольжения при предельной осесимметричной нагрузке
Использовав приближенное очертание поверхностей скольжения в грунте, В.Г. Березанцев рассмотрел условия предельного равновесия для плоской и осесимметричной задач. Им была получена следующая формула для определения среднего предельного давления на основание:
при полосовой нагрузке
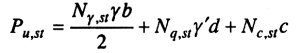 (8.35)
(8.35)
при круглом фундаменте
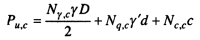 (8.36)
(8.36)
где N — с соответствующими индексами — безразмерные коэффициенты несущей способности, которые принимаются по табл. 8.2, в зависимости от угла внутреннего трения φ; b — ширина ленточного фундамента; D — диаметр круглого фундамента; γ и γ1 — средний удельный вес грунта соответственно ниже и выше подошвы фундамента; d — глубина заложения подошвы фундамента; с — удельное сцепление.
Таблица 8.2. Значения коэффициентов Nγ, Nq, Nc (к расчету по формулам (8.35), (8.36))
| φ, град | При полосовой нагрузке |
При круглом фундаменте | |||||
| Nγ,st | Nq,st | Nc,st | Nγ,c | Nq,c | Nc,c | ||
| 16 | 3,4 | 4,4 | 11,7 | 4,1 | 4,5 | 12,8 | |
| 18 | 4,6 | 5,3 | 13,2 | 5,7 | 6,5 | 16,8 | |
| 20 | 6,0 | 6,5 | 15,1 | 7,3 | 8,5 | 20,9 | |
| 22 | 7,6 | 8,0 | 17,2 | 9,9 | 10,8 | 24,6 | |
| 24 | 9,8 | 9,8 | 19,3 | 14,0 | 14,1 | 29,9 | |
| 26 | 13,6 | 12,3 | 23,2 | 18,9 | 18,6 | 36,4 | |
| 28 | 16,0 | 15,0 | 25,8 | 25,3 | 24,8 | 45,0 | |
| 30 | 21,6 | 19,3 | 31,5 | 34,6 | 32,8 | 55,4 | |
| 32' | 28,6 | 24,7 | 38,0 | 48,8 | 45,5 | 71,5 | |
| 34 | 39,6 | 32,6 | 47,0 | 69,2 | 64,0 | 93,6 | |
| 36 | 52,4 | 41,5 | 55,7 | 97,2 | 87,6 | 120,0 | |
| 38 | 74,8 | 54,8 | 70,0 | 142,5 | 127,0 | 161,0 | |
| 40 | 100,2 | 72,0 | 84,7 | 216,0 | 185,0 | 219,0 | |
| 42 | 154,6 | 98,7 | 108,7 | 317,0 | 270,0 | 300,0 | |
| 44 | 220,6 | 137,2 | 141,2 | - | - | - | |
| 46 | 319,2 | 195,0 | 187,5 | - | - | - | |
Формулами (8.32)-(8.36) можно воспользоваться при осевом приложении нагрузки. В случае приложения внецентренной нагрузки для определения предельного давления необходимо воспользоваться формулами, приведенными в книгах ВТ. Березанцева (1970), Н.А. Цытовича (1983) и др.
Пример 8.1. Определить значения начального критического
давления и среднее предельное давление грунта основания ленточного фундамента
шириной b — 2,0 м, глубиной заложения d = 1,6 м при
характеристиках грунта основания (глины): удельный вес грунта у = 17,5
кН/м3, угол внутреннего трения φ = 18° и удельное сцепление С = 52
кПа.
Решение. Определим начальное критическое давление по формуле (8.28):
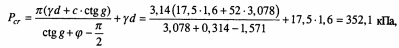
где φ=18·π/180=0,314
Определяем среднее предельное давление грунта по формуле (8.35)
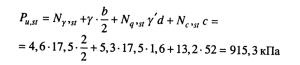
Коэффициенты Nγ,st; Nq,st; Nc,st принимаем по табл. 8.2 при φ = 18°.



